Last week, I wrote about the announcement of the first results from the Alpha Magnetic Spectrometer: a measurement of the positron fraction in cosmic rays. Although AMS-02 wasn’t the first to make this measurement, it was nevertheless a fairly exciting announcement because they confirm a drastic deviation from the theoretical prediction based on known astrophysical sources.

Unfortunately, most of what you can read about it is pretty light on details. News articles and blog posts alike tend to go (1) Here’s what AMS measured, (2) DARK MATTER!!!1!1!! All the attention has been focused on the experimental results and the vague possibility that it could have come from dark matter, but there’s precious little real discussion of the underlying theories. What’s a poor theoretical physics enthusiast to do?

Well, we’re in luck, because on Friday I attended a very detailed presentation on the AMS results by Stephane Coutu, author of the APS Viewpoint about the announcement. He was kind enough to point me to some references on the topic, and even to share his plots comparing the theoretical models to AMS (and other) data, several of which appear below. I never would have been able to put this together without his help, so thanks Stephane!

Time to talk positrons.

The Cosmic Background

When people talk about “known astrophysical sources” of positrons, they’re mostly talking about cosmic rays. Not primary cosmic rays, though, which are the particles that come directly from pulsars, accretion discs, or whatever other sources are out there. Primary cosmic rays are generally protons or atomic nuclei. As they travel through space, they decay into other particles, secondary cosmic rays, through processes like this:

Positrons in the energy range AMS can detect, below \(\SI{1}{TeV}\) or so, mostly come from galactic primary cosmic rays (protons). We can determine the production spectrum of these cosmic ray protons (how quickly they are produced at various energies) using astronomical measurements like the ratio of boron to carbon nuclei and the detected flux of electrons — but that’s a whole other project that I won’t get into here.

Once the proton spectrum is set, we can combine it with the density of the interstellar medium to determine how often reactions like the one above will occur, again as a function of energy. That gives us a spectrum for positron production. But to actually match this model to what we detect in Earth orbit, we need to account for various energy loss mechanisms that affect cosmic rays as they travel. Both primary (protons) and secondary (positrons) cosmic rays lose energy to processes like synchrotron radiation (energy losses as charged particles change direction in a magnetic field), bremsstrahlung (energy losses from charged particles slowing down in other particles’ electric field), and inverse Compton scattering (charged particles “bouncing” off photons). These dissipative mechanisms tend to reduce the positron spectrum at high energies.

Doing all this accurately involves accounting for the distribution of matter in the galactic disk, and accordingly it takes a rather sophisticated computer program to get it right. The “industry standard” is a program called GALPROP, which breaks down the galaxy and its halo (a slightly larger region surrounding the disk, which contains globular clusters and dark matter) into small regions, tracks the spectra of various kinds of particles in each region, and models how the spectra change over time as cosmic rays move from one region to another. There are various models with different levels of detail, most of which are described in this paper and improved in e.g. this one and this one:

• The class of theories known as leaky box models (or homogeneous models) assume that cosmic rays are partially confined within the galaxy — a few leak out into intergalactic space, but mostly they stay within the galactic disk and halo. Both the distribution of where secondary cosmic rays are produced and the interstellar medium they travel through are effectively uniform. Accordingly, the times (or distances) they travel before running into something follow an exponential distribution with an energy-dependent average value \(\expect{t}\) (or \(\lambda_e = \rho v\expect{t}\)).
• The diffusive halo model assumes that the galaxy consists of two regions, a disk and a halo. Within these two regions, cosmic rays diffuse outward from their sources, and those that reach the edge of the halo escape from the galaxy, never to return. The diffusion coefficient is taken to be twice as large in the disk as in the halo due to the increased density of matter.
• The dynamical halo model is exactly like the diffusive halo model with the addition of a “galactic wind” that pushes all cosmic rays in the halo outward at some fixed velocity \(V\).

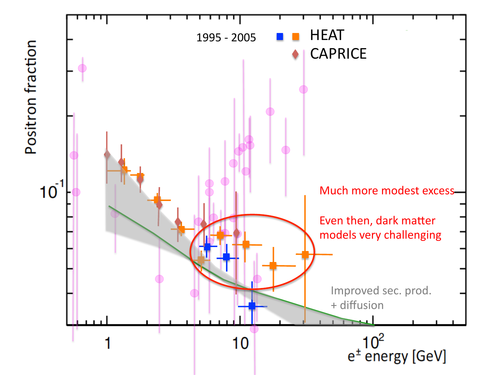
There are others, less commonly used, but all these models share one significant thing in common: they give a positron fraction that decreases with increasing energy. And the first really precise measurements of cosmic ray positrons, performed by the HEAT and CAPRICE experiments, confirmed that conclusion, as shown in this plot.

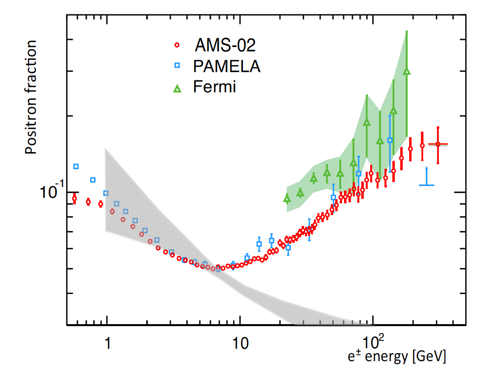
But new data from PAMELA, Fermi-LAT, and now AMS-02 show something entirely different! Above \(\SI{10}{GeV}\), the positron fraction actually increases with energy, showing that something must be producing additional positrons at those higher energies.

The spectrum of the positron fraction excess, i.e. the difference between secondary emission predictions and the data, suggest that this unknown source produces roughly equal numbers of positrons and electrons at the energies AMS has been able to measure, with a power-law spectrum for each:

As an example model, the AMS-02 paper postulated

with \(E_s = \SI{760}{GeV}\) based on a fit to their data. But regardless of whether this specific formula works, the point is that secondary emission tends to produce more positrons than electrons (because most primary cosmic rays are protons, which generally decay into positrons due to charge conservation). That doesn’t fit the profile. This unexplained excess is probably something else.

Neutralinos

Naturally, physicists are going to be most excited if the positron excess turns out to come from some previously unknown particle. The most likely candidate is the neutralino, denoted \(\tilde{\chi}^0\), a type of particle predicted by most supersymmetric theories. Neutralinos are the superpartners of the W and Z gauge bosons, and of the Higgs boson(s).

According to the theories, reactions involving supersymmetric particles tend to produce other supersymmetric particles. The neutralino, as the lightest of these particles , is at the end of the supersymmetric decay chain, which makes it a good candidate to constitute the mysterious dark matter. But occasionally, neutralinos will annihilate to produce normal particles like positrons and electrons. If dark matter is actually made of large clouds of neutralinos, it’s natural to wonder whether the positrons produced from their annihilation could make up the difference between the prediction from secondary cosmic rays and the AMS observations.

Here’s how the calculation goes. Using the mass of dark matter we know to exist from galaxy rotation curves and gravitational lensing, and assuming some particular mass \(m_{\chi}\) for the neutralino, we can calculate how many neutralinos are in our galaxy’s dark matter halo. Multiplying that by the decay rate predicted by the supersymmetric theory gives the rate of positron production from neutralino decay. That rate gets plugged into cosmic ray propagation models like those described in the last section, leading to predictions for the positron flux measured on Earth.

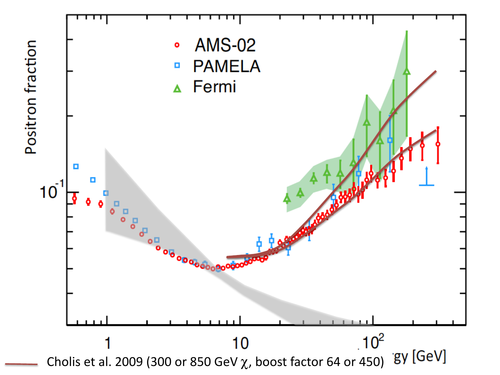
Several teams have run through the calculations and found that… well, it kind of works, but only if you fudge the numbers a bit. Neutralino annihilation predicts a roughly power-law contribution to the positron fraction up to the mass of the neutralino; that is,

As long as \(m_\chi \gtrsim \SI{500}{GeV}\) or so, this is exactly the kind of spectrum needed to explain the discrepancy between the PAMELA/Fermi/AMS results and the secondary emission spectrum. The problem lies in the overall constant \(C\), which you would calculate from the dark matter density and the theoretical decay rate. It’s orders of magnitude too small. So the papers multiply this by an additional “boost” factor, \(B\), and examine how large \(B\) needs to be to match the experimental results. Depending on the model, \(B\) ranges from about 30 (Baltz et al., \(m_\chi = \SI{160}{GeV}\)) to over 7000 (Cholis et al., \(m_\chi = \SI{4000}{GeV}\)).

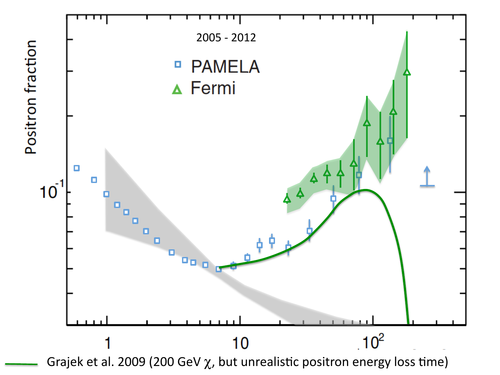
Alternatively, you can assume that something is wrong with the propagation models, and that positrons lose more energy than expected on their way through the interstellar medium. This is the approach taken in this paper, which finds that increasing the energy loss rate by a factor of 5 can kind of match the positron fraction data.

But that much of an adjustment to the energy loss leads to conflicts with other measurements. It winds up being an even more unrealistic model.

Even if the parameters of some supersymmetric theory can be tweaked to match the data without a boost factor, there’s one more problem: neutralinos decay into antiprotons and photons too. If the positron excess is caused by neutralino decay, there should be corresponding excesses of antiprotons and gamma rays, but we don’t see those. It’s going to be quite tricky to tune a dark matter model so that it gives us the needed flux of positrons without overshooting the measurements of other particles. There is only a small range of values of mass and interaction strength that would be consistent with all the measurements. So as much as dark matter looks like an interesting direction for future research, it’s not a realistic model for the positron excess just yet.

Astrophysical sources

With the dark matter explanation looking only moderately plausible at best, let’s turn to other (less exotic) astrophysical sources. There’s a fair amount of uncertainty about just how many cosmic rays are produced even by known sources. They could be emitting enough electrons and positrons to make the difference between the new data and the theories.

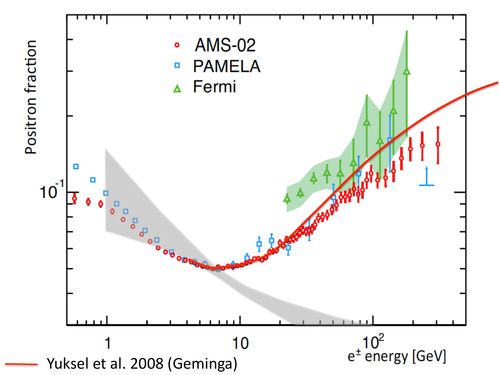
Pulsars in particular, in addition to being sources of primary cosmic rays (protons), are often surrounded by nebulae that emit electrons and positrons from their outer regions. The pulsar’s solar wind interacts with the nebula to accelerate light particles to high energies, giving these systems the name of pulsar wind nebulae (PWNs). Simply by virtue of being a PWN, it’s expected to emit a certain “baseline” positron and electron flux, which is included in secondary emission models, but the pulsar could have been much more active in the past, emitting a lot more positrons and electrons. These would have become “trapped” in the surrounding nebula and continued to leak out over time, which means we would be seeing more positrons and electrons than we’d expect to based on the pulsar’s current activity. There are a few nearby PWNs which seem like excellent candidates for this effect, going by the (rather snazzy, if you ask me) names of Geminga and Monogem. A number of papers (Yüskel et al., and recently Linden and Profumo) have crunched the numbers on these pulsars, and they find that the positron/electron flux from enhanced pulsar activity can match up quite well with the positron fraction excess detected by PAMELA, Fermi-LAT, and AMS-02.

The “smoking gun” that would definitely (well, almost definitely) identify a pulsar as the source of the excess would be an anisotropy in the flux: we’d see more positrons coming from the direction of the pulsar than from other directions in the sky. Now, AMS-02 (and Fermi-LAT before it) looked for an effect of this sort, and they didn’t find it — but according to Linden and Profumo, it’s entirely possible that the anisotropy could be very slight, less than what either experiment was able to detect. We’ll have to wait for future experimental results to check that hypothesis.

Modified secondary emission

Of course, it’s important to remember (again) that all these analyses are based on the propagation models that tell us how cosmic rays are produced and move through the galaxy. It’s entirely possible that adjusting the propagation models alone, without involving any extra source of positrons, would bring the predictions from secondary emission in line with the experimental data.

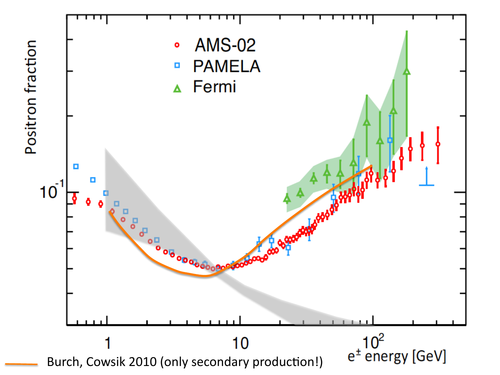
A paper by Burch and Cowsik looked at this possibility, and it turns out that something called the nested leaky-box model can fix the positron fraction discrepancy fairly well. As I wrote back in the first section, the leaky box model gets its name because cosmic rays are considered to be partially confined within the galaxy. Well, the nested leaky box model adds the assumption that cosmic rays are also partially confined in small regions around the sources that produce them. That means that, rather than being produced uniformly throughout the galaxy, secondary cosmic rays come preferentially from certain regions of space. This is actually similar to the hypothesis from the last section, of extra positrons coming from PWNs, so it shouldn’t be too surprising that using the nested leaky box model can account for the data about as well as the pulsars can.

Looking to the future

All the media outlets reporting on the AMS results have been talking about the dark matter hypothesis, even going so far as to say AMS found evidence of dark matter — but clearly, that’s not the case. There’s no reason to say we have evidence of dark matter when there are perfectly valid, simpler, maybe even better explanations for the positron fraction excess at high energies! There’s just not enough data yet to tell which explanation is right.

As AMS-02 continues to make measurements over the next decade or so, there are two main things to look for that will help distinguish between these models. First, does the positron fraction stop rising? And if so, where on the energy spectrum does it peak? As we’ve seen, this can happen in any model, but if neutralino annihilation is the right explanation, that peak will have to occur at an energy compatible with other constraints on the neutralino mass. Perhaps more importantly, is there any anisotropy in the direction from which these positrons are coming? If there is, it would pretty strongly disfavor the dark matter hypothesis. The anisotropy itself could actually point us toward the source of the extra positrons. So even if we don’t wind up discovering a new particle from this series of experiments, there’s probably something pretty interesting to be found.