When I arrived in Princeton last Friday, I was greeted with this headline:

Emergency meningitis vaccine will be imported to halt Ivy League outbreak

Emergency doses of a meningitis vaccine not approved for use in the U.S. may soon be on the way to Princeton University to halt an outbreak of the potentially deadly infection that has sickened seven students since March.

Well then. Perfect timing. But seriously, it is actually a perfect time to reflect on why vaccines are necessary in the first place. And it’s not (just) for the reason you might think.

If you’re vaccinated against a disease, not only does it mean that you won’t get sick, it also means that you won’t pass that disease on to other people. Vaccinations protect the people around you too. And conversely, even if you’re not vaccinated yourself, the more people around you who are, the lower your chances of catching the disease from someone else.

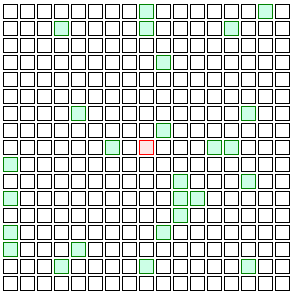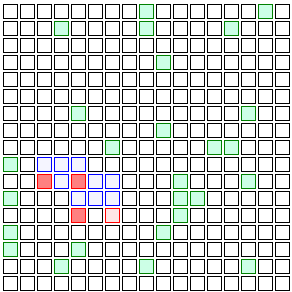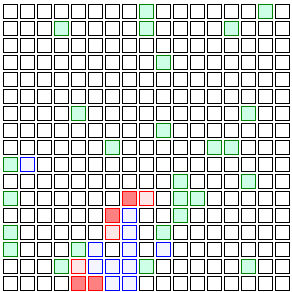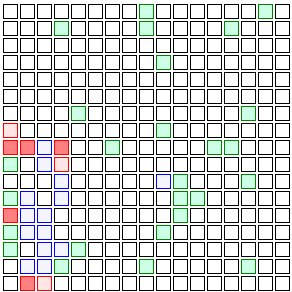
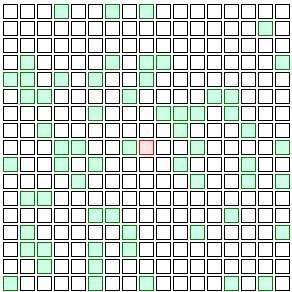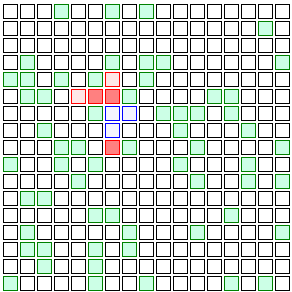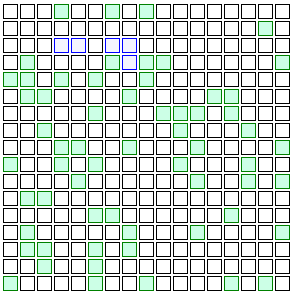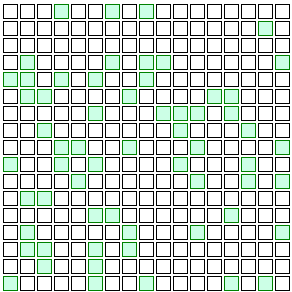
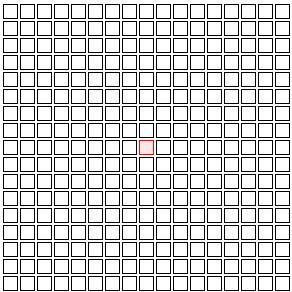
Let me illustrate this with a simple model of how a disease spreads. Imagine a world where people live in apartments on a perfect grid and only ever talk to their four neighbors, once a day.

Suppose one of these people gets sick.

Each time that person talks to their neighbor, they have some chance to pass on the disease. Maybe each day that they’re sick, the person has a 20% chance to infect each neighbor. (That’s a pretty high chance, but then again in reality most of us talk to a lot more than four people each day.) If the illness lasts three days, the odds are pretty good that one or two neighbors are going to get infected.

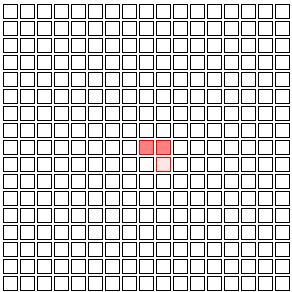
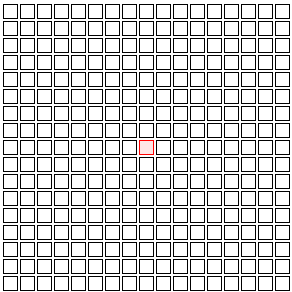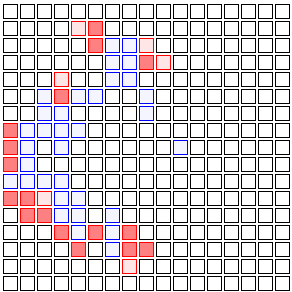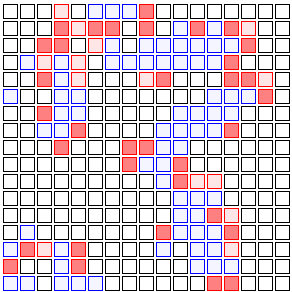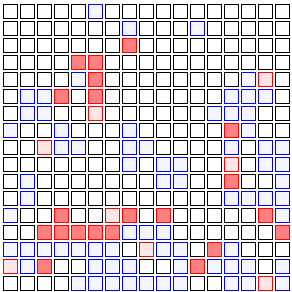
(light red squares represent people who have just gotten sick, dark red represent those who have been sick for a while)

And then those neighbors infect their neighbors. The four neighbors of Patient Zero (the first person to get sick) have eight new neighbors of their own, so there are even more opportunities for the infection to spread.

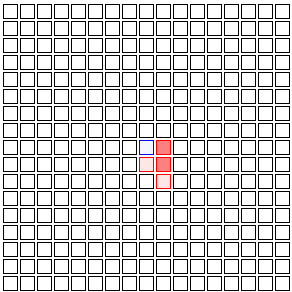
(blue squares represent people who are recovering)

And then those eight neighbors have 12 new neighbors, and those 12 have 16, and so on. Eventually you wind up with a wave of infection spreading back and forth through the population.

What if some of these people are vaccinated?

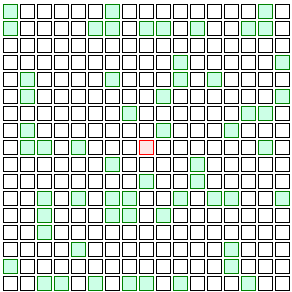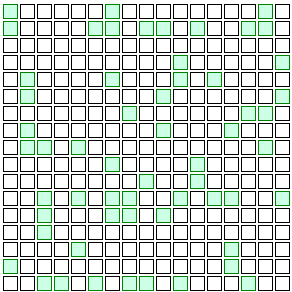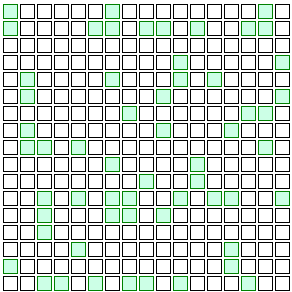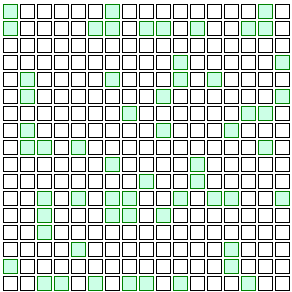
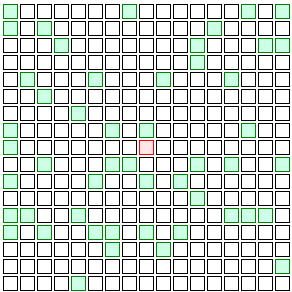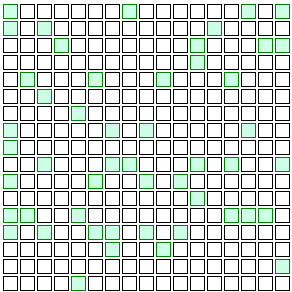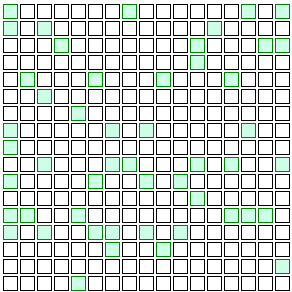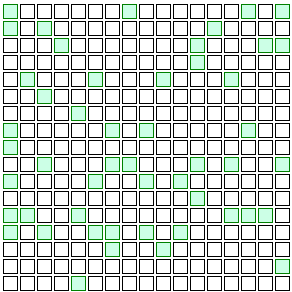
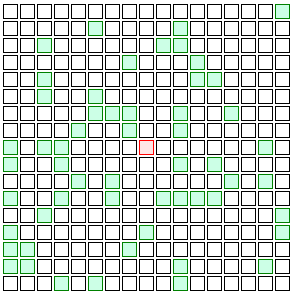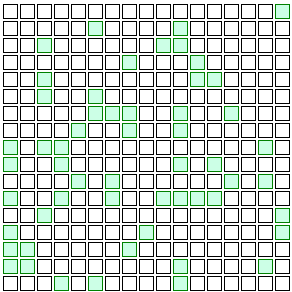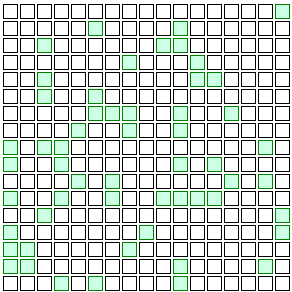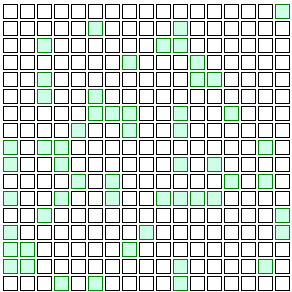
Vaccines don’t work on everyone in real life, but to keep my example simple, I’ll pretend vaccinated people are totally immune to the disease. They’ll be represented by green squares. Look what happens if even 10% of the people in this imaginary grid city are vaccinated:

See the difference? The infection finds it a lot harder to spread. Instead of disease running rampant throughout the population, it’s limited to one little cluster in a corner of the grid. The few people who are vaccinated act as a protective barrier of sorts — maybe one with a few holes in it, but still, enough to significantly hold back the spread of the disease and keep the unvaccinated 90% a lot safer.

Say we increase that to 20% of people getting vaccinated. Here’s what that looks like:

Now how about that! The disease just sputters out without ever reaching most of the population!

Maybe that was just a fluke. Let’s try again and let the randomness play out differently:

Same thing. One more:

Yet again, the infection disappears after just a few steps of the simulation.

Wait — I lied. Watching these little colored squares is too entertaining. This is the last one I swear:

It takes a little longer this time, but still, the infection disappears.

Evidently, you only need some critical fraction of the population to be vaccinated to stop a communicable disease in its tracks! This phenomenon is called herd immunity.

The critical fraction of vaccinated people you need to produce herd immunity depends on how people in the population interact with each other. In my toy example, there’s very little interaction — each person only interacts with four neighbors, once a day. That makes the critical fraction fairly low; just 20% vaccinated is enough to stop the disease after a fairly short time.

In real life, people interact a lot more, which means the critical fraction is higher: 80%, 90%, 95%, or more. A community can only afford to leave a few people unvaccinated without spoiling the herd immunity. It’s important to leave those “slots” for those few people who have legitimate medical reasons not to take a vaccine, so that they can be protected by the rest of us.

For the curious, here is the (completely unpolished) Python code I used to create the pictures.