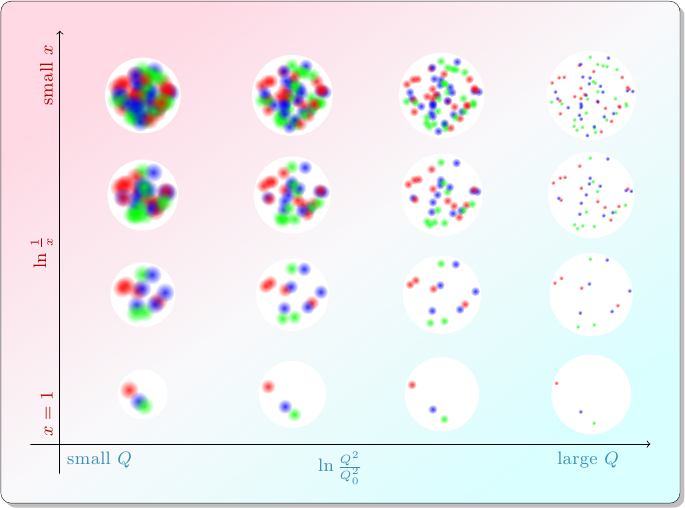
Time to kick off a new year of blog posts! For my first post of 2015, I’m continuing a series I’ve had on hold since nearly the same time last year, about the research I work on for my job. This is based on a paper my group published in Physical Review Letters and an answer I posted at Physics Stack Exchange.

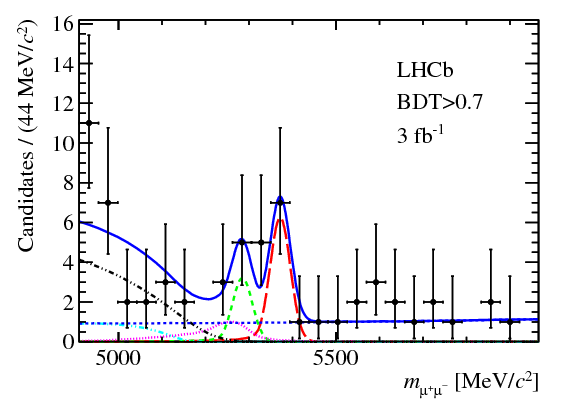
In the first post of the series, I wrote about how particle physicists characterize collisions between protons. A quark or gluon from one proton (the “probe”), carrying a fraction \(x_p\) of that proton’s momentum, smacks into a quark or gluon from the other proton (the “target”), carrying a fraction \(x_t\) of that proton’s momentum, and they bounce off each other with transverse momentum \(Q\). The target proton acts as if it has different compositions depending on the values of \(x_t\) and \(Q\): in collisions with smaller values of \(x_t\), the target appears to contain more partons.

At the end of the last post, I pointed out that something funny happens at the top left of this diagram. Maybe you can already see it: in these collisions with small \(x_t\) and small \(Q\), the proton …

Hooray, it’s time for science! For my long-overdue first science post of 2014, I’m starting a three-part series explaining the research paper my group recently published in Physical Review Letters. Our research concerns the structure of protons and atomic nuclei, so this post is going to be all about the framework physicists use to describe that structure. It’s partially based on an answer of mine at Physics Stack Exchange.

What’s in a proton?

Fundamentally, a proton is really made of quantum fields. Remember that. Any time you hear any other description of the composition of a proton, it’s just some approximation of the behavior of quantum fields in terms of something people are likely to be more familiar with. We need to do this because quantum fields behave in very nonintuitive ways, so if you’re not working with the full mathematical machinery of QCD (which is hard), you have to make some kind of simplified model to use as an analogy.

If you’re not familiar with the term, fields in physics are things which can be represented by a value associated with every point in space and time. In the simplest kind of …

You’ve probably heard that the Nobel Prize in Physics was awarded yesterday to François Englert and Peter Higgs, for the theoretical prediction of the Higgs boson. You’ve probably also heard all the commotion leading up to the announcement, about how silly it is that Nobel Prizes are awarded only to three people. And you may have noticed that I didn’t weigh in.

Frankly, that’s because I didn’t really care. I’m sure it’s a big deal to the recipients and non-recipients of the prize, but to the rest of us, the work done by all six authors stands on its own merits. The community of physicists doesn’t need a prize to tell them whose research leads to a better understanding of the universe — and in the end, even if you ask most Nobel Prize winners, understanding the universe is what makes doing science worthwhile, not getting recognition.

If this year’s debate gets people to look more closely at the actual science being done, and put less emphasis on who gets labeled a Nobel Prize winner, that can only be a good thing.

I’ll leave you with the links to the Nobel-winning …

Time for a blog post that has been far too long coming! Remember the Quest for B Meson Decay? I wrote about this several months ago: the LHCb experiment had seen one of the rarest interactions in particle physics, the decay of the \(\mathrm{B}^0_s\) meson into a muon and antimuon, for the first time after 25 years of searching.

Lots of physicists were interested in this particular decay because it’s unusually good at distinguishing between different theories. The standard model (which incorporates only known particles) predicts that a muon and antimuon should be produced in about 3.56 out of every billion \(\mathrm{B}^0_s\) decays — a number known as the branching ratio. But many other theories that involve additional, currently unknown particles, predict drastically different values. A precise measurement of the branching ratio thus has the ability to either rule out lots of theoretical predictions, or provide the first confirmation on Earth of the existence of unknown particles!

Naturally, most physicists were hoping for the latter possibility — having an unknown particle to look for makes things exciting. But so far, the outlook doesn’t look good. Last November, LHCb announced their measurement of the branching ratio …

Hooray, it’s time for another blog post! What I’m writing about this time is kind of old news — and don’t worry, there’s more to come on just why I haven’t been able to write about it for so long — but very interesting nonetheless.

A few weeks ago, two separate physics experiments announced that they had discovered a tetraquark, a composite particle made of four quarks. Or rather, that’s what all the popular news coverage said. But what really happened? The discovery of a real tetraquark would be huge news, so I’m sure not going to trust the media reports on this one. As always, I’m going straight to the source: the original papers by the BES III and Belle collaborations.

Two or Three is Company, Four’s a Crowd

Before delving into the discovery itself, I’m going to tackle the burning question on everybody’s mind: what’s so special about a particle made of four quarks?

To understand that, we have to look to quantum chromodynamics (QCD), the theory of how “color-charged” particles interact. In some ways, QCD is superficially similar to quantum electrodynamics, the theory of how electrically charged …

It’s that time again: Mythbusters is back! And they sure know how to kick things off with a bang — or better yet, a prolonged burn!

For the 10th anniversary of the show, the Mythbusters revisited the very first myth they ever tested, the JATO rocket car. Wikipedia has the story in what appears to be its most common form:

The Arizona Highway Patrol came upon a pile of smoldering metal embedded into the side of a cliff rising above the road at the apex of a curve. the wreckage resembled the site of an airplane crash, but it was a car. The type of car was unidentifiable at the scene. The lab finally figured out what it was and what had happened.

It seems that a guy had somehow gotten hold of a JATO unit (Jet Assisted Take Off - actually a solid fuel rocket) that is used to give heavy military transport planes an extra ‘push’ for taking off from short airfields. He had driven his Chevy Impala out into the desert and found a long, straight stretch of road. Then he attached the JATO unit to his car, jumped in, got up some speed and fired off the …

Last week, I wrote about the announcement of the first results from the Alpha Magnetic Spectrometer: a measurement of the positron fraction in cosmic rays. Although AMS-02 wasn’t the first to make this measurement, it was nevertheless a fairly exciting announcement because they confirm a drastic deviation from the theoretical prediction based on known astrophysical sources.

Unfortunately, most of what you can read about it is pretty light on details. News articles and blog posts alike tend to go (1) Here’s what AMS measured, (2) DARK MATTER!!!1!1!! All the attention has been focused on the experimental results and the vague possibility that it could have come from dark matter, but there’s precious little real discussion of the underlying theories. What’s a poor theoretical physics enthusiast to do?

Well, we’re in luck, because on Friday I attended a very detailed presentation on the AMS results by Stephane Coutu, author of the APS Viewpoint about the announcement. He was kind enough to point me to some references on the topic, and even to share his plots comparing the theoretical models to AMS (and other) data, several of which appear below. I never would have been …

A fair amount of what I write about here is about accelerator physics, done at facilities like the Large Hadron Collider. But you can also do particle physics in space, which is filled with fast-moving particles from natural sources. “All” you need to do is build a particle detector, analogous to ATLAS or CMS, and put it in Earth orbit. That’s exactly what the Alpha Magnetic Spectrometer (AMS) is. Since 2011, when it was installed on the International Space Station, AMS has been detecting cosmic electrons and positrons, looking for anomalous patterns, and today they presented their first data release.

Let’s jump straight to the results:

This plot shows the number of positrons with a given energy as a fraction of the total number of electrons and positrons with that energy, \(\frac{N_\text{positrons}}{N_\text{electrons} + N_\text{positrons}}\). The key interesting feature, which confirms a result from the previous experiments PAMELA and Fermi-LAT, is that the plot rises at energies higher than about \(\SI{10}{GeV}\). That’s not what you’d normally expect, because most physical processes produce fewer particles at higher energies. (Think about it: it’s less likely that you’ll accumulate …

Oh, I kid. Despite the name, nothing about this post is a prank (except perhaps for the title).

It’s been a week and a half since the Planck collaboration released their measurements of the cosmic microwave background. At the time, I wrote about some of the many other places you can read about what those measurements mean for cosmology and particle physics. But it’s a little harder to find information on how we come to those conclusions. So I thought I’d dig into the science behind the cosmic microwave background: how we measure it and how we manipulate those measurements to come up with numbers.

Measuring the CMB

With that in mind, what did Planck actually measure? Well, the satellite is basically a spectrometer attached to a telescope. It has 74 individual detectors, each of which detects photons in one of 9 separate frequency ranges. As the telescope points in a certain direction, each detector records how much energy carried by photons in its frequency range hit it from that direction. The data collected would look something like the points in this plot:

From any one of these data points, given the frequency and the measured power …