Yep, that’s right, a rocket-propelled grenade finally made its way on Mythbusters! Personally I’m surprised it took them so long…

Anyway, let’s not get distracted from the science by cool explosions just yet. On last week’s season premiere of Mythbusters, Kari, Tory, and Grant tested a myth based on a scene in RED in which two characters are facing off, one (the hero) with a revolver and the other (the villain) with an RPG launcher. In the movie, they both shoot at the same time, the bullet hits the RPG in midair and detonates it, and the resulting explosion kills the villain. Now, in the show, this myth was busted on several counts:

• RPGs don’t even arm until about 60 feet after launch, about \(\frac{3}{4}\) of the way to the target and long after this one would have been hit by the bullet
• When an RPG explodes, it sends balls of molten copper flying forward, which wouldn’t have been stopped by the bullet
• The distance at which the explosion would have taken place, 16 feet from the villain, is quite survivable

Unfortunately, they didn’t test what I thought was the most obvious objection to the scene (albeit the one that gives it its “cool factor”): you’d need excellent aim, and some amount of luck, to reliably hit as small a target as an RPG detonator head on with a bullet. Or so it seems. But is this really the case? Even if the RPG was armed, and even if it somehow could lose all its forward momentum and explode in a giant fireball, how likely is it that the collision would actually take place?

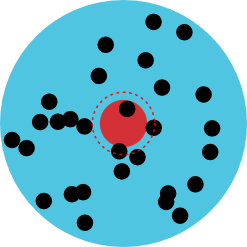As it turns out, shooting two objects at each other and characterizing what happens is a very common thing to do in physics — for instance, this is exactly what happens at particle accelerators like the recently departed Tevatron or the LHC — so the methods used to analyze this sort of situation are quite well studied, especially in a simple case like this one. Imagine the collision from the point of view of the RPG, which “sees” a bullet coming at it. Actually, imagine doing this experiment many times to get a statistical sample, so the RPG actually sees a whole beam of bullets coming at it, as shown on the left. The detonator cap occupies a circle (the solid red one) somewhere in the middle of the beam, and any bullet that hits that circle will trigger an explosion. It’s probably safe to say that even a glancing blow will be enough to set the RPG off, so we should expand that circle a little, specifically by half the radius of a bullet, so that any bullets whose centers are within the circle will cause explosions — that’s the dashed circle in the diagram. The area of this circle is called the scattering cross section, \(\sigma\).

In order to figure out the probability of a collision, we need to find the fraction of bullets that will hit the aforementioned circle. The transverse positions of the bullets relative to the RPG form some distribution, called the beam profile \(\rho(\mathbf{r}_\perp)\), so we can figure out the probability by integrating the beam profile over the circle to get the number of bullets (out of this large statistical sample) that will hit.

So if we can get the normalized beam profile \(\rho(\mathbf{r}_\perp)\) of a stream of bullets, we’d be all set. This is the tricky part, though, since doing so would require looking up some statistics on the accuracy of handgun aiming, and I’m not sure where to get reliable information about that. So in lieu of that, I turn to the internet. Here’s a thread about accuracy at The Firing Line forums which includes some photos of shots made at a specified range. I can extract the coordinates of the bullet holes, compare them to the given scale, and thereby find the beam profile of the person who shot them. Sure, it’s not a statistically significant sample, but I’m just going for a rough estimate anyway.

Since this isn’t a rigorous experiment, I’m just going to work from this one image.

In order to easily determine the coordinates of the bullet holes, I turned to the first tool I had at hand, Mathematica. This little bit of code (for Mathematica 8) will let you click on each hole (or any point) and print out a list of the coordinates you clicked:

DynamicModule[{p = {}}, 
 EventHandler[
   Dynamic@Show[i, Graphics[{PointSize[Large], Red, Point[p]}]], 
   "MouseClicked" :> {AppendTo[p, 
      MousePosition["GraphicsAbsolute"]]}]
  Button["Clear", {p = {}}]
  Button["Print", Print[p]]
 ]

With this I got the following list of positions:

{{280.5,498.},{236.5,447.},{290.5,407.},{335.5,330.},{391.5,449.},{405.5,471.},
 {516.5,409.},{439.5,292.},{299.5,264.},{373.5,227.},{413.5,198.},{453.5,150.},
 {505.5,256.},{554.5,268.},{531.5,132.}}

I also determined that the distance corresponding to the 5.5 inch line marked at the bottom is 316 pixels, which I can use to convert the pixel positions into centimeters. After that, we have to make a distance correction: the picture shows shots taken at a distance of 150 feet, but the scenario in the movie involved a shot of 64 feet, so (as a simple approximation) we just insert a factor of \(\frac{64}{150}\).

This code graphs the fraction of bullet holes as a function of distance from the average bullet position, rescaled to a 64 foot shot:

Histogram[64./150. (EuclideanDistance[Mean[points], #] & /@ points), 10, "CDF"]

Here’s a fancier version:

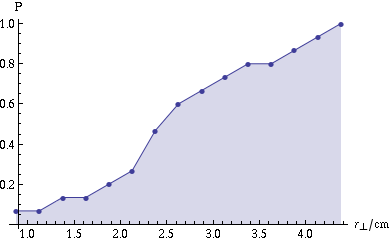
This graph is an approximation to what I would call the cumulative radial beam profile, which is related to the actual beam profile as

Because of the small number of shots I’ve analyzed, it’s hard to tell from the graph exactly what the form of \(\rho_\text{cuml}(R)\) is — it could be linear, or quadratic (as you’d expect for a uniform distribution over a circle), or perhaps Gaussian (although I would expect more clustering in the center if that were the case), or something else entirely.

Thankfully, we don’t really need to know the form, at least not if we just want a rough estimate of the probability. Just set \(R\) to the radius of the scattering cross-section of the detonator cap, and \(\rho_\text{cuml}(R)\) is the probability of hitting it. From what I saw in the show, I’d estimate \(R \approx \SI{2.5}{cm}\), which puts the probability at \(P \approx 0.5\). That’s actually not a bad chance — not one I’d want to stake my life on, but a lot better than I would have guessed. And according to this article on handgun accuracy from Guns & Ammo magazine, it seems like that’s average for a skilled casual shooter. I bet a trained CIA agent, especially one worthy of being played in a movie by John Malkovich, would have no problem making the shot.