I am a “retired” postdoc in particle physics, trying to transition into the tech industry. I started out programming with Java around 1999, and more recently I’ve been doing a lot of work with Python, C, and C++, although I do occasionally dabble in PHP, Perl, shell scripting, and other languages.
Hooray, it works again! It took about 3 days of frantic hacking in the free time I had left over from research, but my website is back up and working properly (so it seems) on the new server. More blog posts to come, when I have time. Soon, I promise.
That is all.
The (virtual) computer this site runs on is showing its age, so I’m switching over to a newer one within the next day or so. Just so you know in case you have any trouble accessing the site.
While I’m on the subject, kudos to Linode for having a very solid migration plan and for making continual upgrades to their hardware while lowering prices. The new server costs about a third as much as the one I’m using now.
Today I’m announcing pwait, a little program I wrote to wait for another program to finish and return its exit code. Download it from Github and read on…
Because I was procrastinating one day and felt like doing some systems programming.
Seriously though. Sometimes you need to run one program after another one finishes. For example, you might be running a calculation and then you need to run the data analysis script afterwards, but only if the calculation finished successfully. The easy way to do this is
run_calculation && analyze_data
(sorry to readers who don’t know UNIX shell syntax, but then again the program I’m introducing is useless to you anyway).
Which is fine if you plan for this before you run the calculation in the first place, but sometimes you already started the calculation, and it’s been running for 3 hours and you don’t want to stop it and lose all that progress. The easy way to do this is to hit Ctrl+Z (or some equivalent; it depends on your terminal) to suspend the calculation, and then run
fg && analyze_data
which will resume it and run the analysis script afterwards.
Which is …
Join the Google group mailing list to stay informed or to help with planning!
My post last week considering options for a new science communication conference series got a pretty strong response, at least relative to most things on this blog. As it turns out, there already are some people in various stages of planning new (un)conferences in the style of Science Online, much like what I was thinking about. I won’t say anything about them here because those people haven’t revealed their plans yet, but I hope they will go public soon!
I also completely forgot that Science Online was not monolithic; it had regional branches around the US and around the world, which were largely separate from the main organization. At least two of them are still holding events: Science Online Leiden and Science Online DC. (There are also branches in Boston, Denver, and Vancouver, maybe others that I don’t know about, but they seem to be inactive.) These smaller groups could play a big role in the future of the science communication community, since as several people have pointed out, it’s a lot easier to organize events that involve fewer people. Perhaps …
My boss got me a new toy today.
This is one of the perks of working for a well-funded research group, I guess. And a new research group. It’s not often that you get your foot in the door right when they’re buying equipment.
It’s also a perk of being a phenomenologist (which is like being a theorist but sometimes we measure things we can’t calculate). Unlike experimental physicists, who have to spend their budgets on all sorts of exotic lab equipment (which I’m given to understand means obscene amounts of duct tape and aluminum foil), all you need for phenomenology is a computer, pencil and paper, and a place to sit. So there’s really no reason not to blow as much money as possible on nice equipment. And this is nice equipment. It’s literally the best Apple computer you can buy over here, featuring a 27 inch display (oooooh) and OS X Yosemite, the newest update to the operating system.
Not that I don’t have reason to complain. The system stalled twice before I even managed to finish the setup procedure.
I guess I have to start making offerings to the …
Quick, what’s wrong with this C++ program?
#include <iostream>
int test(int arg) {
cout << arg << endl;
}
int main(int argc, char** argv) {
test(5);
}
Did you guess nothing at all? Because that’s what GCC says:
$ g++ -o funnyprogram funnyprogram.cpp
$
WTF.
Pretty much every other programming language that makes you explicitly identify a function’s return type will also make you actually return something from that function. C and C++ don’t, and furthermore GCC doesn’t even warn you that anything is wrong. This can occasionally lead to serious bugs, as I discovered today in this real-world example. I had a function that checks the name of an object and returns an enum value based on that name.
virtual const HardFactorOrder get_order() const {
// relies on a particular convention for get_name()
// but can be overridden for hard factors where that convention doesn't apply
std::string name = get_name();
if (name.compare(0, 3, "H01") == 0) {
return MIXED;
}
else if (name.compare(0, 2, "H0") == 0) {
return LO;
}
else if (name.compare(0, 2, "H1") == 0) {
return NLO;
}
};
That was all good when all the objects involved had names conforming to the convention, but my latest batch of updates to …
I’m having a little too much fun with my newly-discovered ability to embed Twitter widgets. Enjoy these scientific twists on popular movie titles.
Math is hard.
Not for Barbie, but for Mathematica.
I ran into a weird Mathematica bug while trying to evaluate the sum
Split this into three parts. The first one is the well-known expansion of the exponential function
The second is not the well-known expansion of the exponential function.
Obviously not, in fact, since if two power series are equal, \(\sum_i a_n z^n = \sum_i b_n z^n\), for an infinite number of points, each of their coefficients have to be equal: \(\forall n,\ a_n = b_n\). (You can show this by taking the difference of the two sides and plugging in a bunch of different values of \(z\).)
I guess Mathematica doesn’t know that.
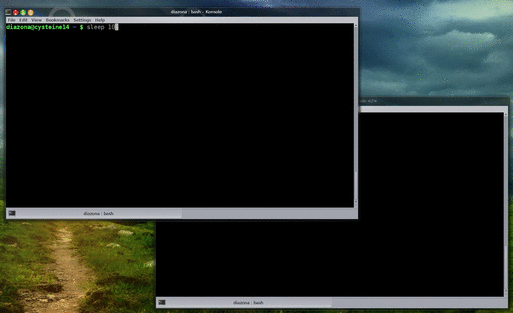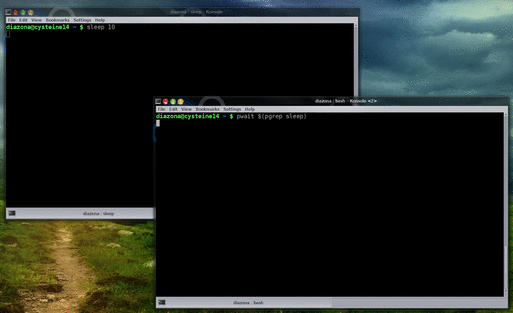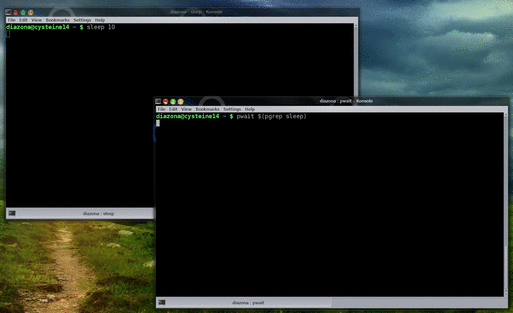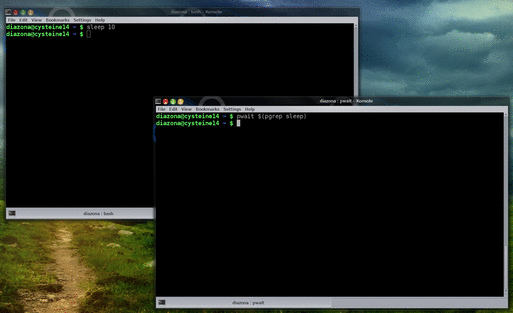
In[1] = Sum[PolyGamma[1, k + 1] z^k/k!, {k, 1, Infinity}]
Out[1] = 1/6(-1 + E^z)Pi^2
I had my hopes up for …
It’s been a little more than a month since Science Online, the organization famous for its annual series of conferences (and infamous for the sexual harassment promulgated by one of its founders) announced that it was disappearing for good. I don’t see anyone else making serious plans for a successor to Science Online Together, so I’m going to push for this myself. These are my thoughts....
Hey, internet. Long time no see.
(It’s often claimed “long time no see” is a literal translation from Chinese “好久不见”, “hǎo jiǔ bú jiàn”, but actually nobody knows for sure.)
On Thursday, my computer crashed. Not just that it crashed, but it somehow corrupted itself so that I couldn’t even boot it. It survived for two seconds after being turned on, before bailing out with this error:
init[1]: segfault at 0 ip 00007ff10ea3fe05 sp 0007ffff7cb49148 error 4 in libc-2.19.so[7ff10e919000+19e000]
Kernel panic - not syncing: Attempted to kill init! exitcode=0x0000000b
This is so early in the startup process that nothing is running. It’s pretty much just the kernel and init (which, if you don’t know, is the very first program to run when a Linux system starts, the one that runs all other programs).
So of course I recompiled (it’s Gentoo) and reinstalled both the kernel and init, as well as libc, several times, as well as several other programs that I’m pretty sure didn’t even get a chance to start, so how could they have anything to do with this crash? Still, better safe than sorry I guess …