OK, maybe it’s not what you think, the CAS‘s of the world are not going to rise up and enslave us :-P (Not yet, anyway.) But it is always a good idea to view their results with a healthy dose of skepticism, because like any computer program, they have bugs, and every once in a while one can actually mess up your calculation.

Here’s my example:

Plug this into Mathematica 8.0 and it will tell you that the integral is equal to \(2\pi i J_1(k)\), where \(J_1\) is a Bessel function of the first kind:

In[1]  := Integrate[Cos[x] Exp[I k Cos[x - y]], {x, 0, 2 Pi}]
Out[1] := ConditionalExpression[2 I \[Pi] BesselJ[1, k], k \[Element] Reals]

But it’s not! If you shift the integration variable \(x\to x + y\), Mathematica tips its hand and tells you the real answer, \(2\pi i J_1(k)\cos y\):

In[2]  := Integrate[Cos[x + y] Exp[I k Cos[x]], {x, 0, 2 Pi}]
Out[2] := 2 Pi I BesselJ[1, k] Cos[y]

You can also do …

Today the internet is abuzz with the news that the papers from ATLAS and CMS announcing their discovery of the Higgs boson have passed peer review and are officially published in Physics Letters B. That means now they’re actual science, right?

Not really. (I’m assuming the ExtremeTech headline was a bit of a joke.) Peer review is really not as big of a deal as people outside the scientific community are often led to think. In particular, “peer-reviewed” does not mean “correct.” Peer review is just a high-level check to make sure that the paper isn’t complete nonsense and that the problem it’s addressing is relevant and interesting. Journals have limited space to publish these things, and they have to determine which of the many submissions they get are the most worthy of being put in that space. That’s what the peer review process is for.

When something comes out of a big experimental collaboration like ATLAS or CMS, though, it has already gone through a rigorous vetting process. Doubly so for a high-profile result like this one — in fact, I’m sure the results had been double- and triple-checked by dozens of people even …

You may have noticed that instead of delivering the summary of Quark Matter 2012 I promised in my last post, I disappeared from the blog for a few weeks. Unfortunately I got involved in some research work immediately after coming back, which left me with zero time for blogging anything longer than 140 characters.

Well, all that ends now. I’ve already written about the main results from Quark Matter, and that post already encompasses much of what was presented over the rest of the week, but I do want to mention a couple of significant activities that weren’t part of the conference proper.

First, on Thursday evening we were treated to a banquet in the Omni Shoreham’s main ballroom, followed by a popular science talk from Phil Plait, the guy behind the Bad Astronomy blog. In sharp contrast to the dense technical talks of the rest of the conference, this one was incredibly entertaining. If you ever get the chance to see him talk about his new book on cosmic disasters, I highly recommend it. I mean, how can you not enjoy half an hour spent making fun of the bad science in Armageddon? (also the subject …

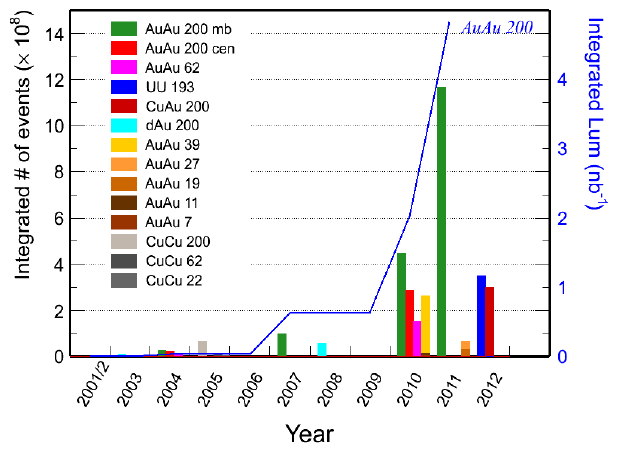
We’re now halfway into Quark Matter 2012, and many of the presentation slots (at least the ones I’ve looked at) have been devoted to the experimental groups presenting their new results. In heavy ion physics, the major groups are the STAR and PHENIX collaborations at RHIC, and ATLAS, CMS, and ALICE (which I’ve learned is pronounced “ah-LEES,” not “AL-iss”) at the LHC.

Naturally, the experts who are interested in these things will just go straight to the conference page and look at the presentations — heck, they’re pretty much all here in Washington anyway. So I’m going to try to explain some of these results in a way that makes them comprehensible for non-experts (although, apparently unlike some of my fellow conferencegoers, I’ll give you enough credit to assume you know what atoms are).

What Quark Matter is all about

The main focus of the Quark Matter conference is, of course, quarks, and also gluons: the most fundamental particles that make up atomic nuclei. How do they organize themselves into protons and neutrons and then into nuclei? How do the properties of those atomic nuclei emerge from their internal structure? And what really happens when …

Quark Matter the conference proper kicked off this morning (yeah, it was actually yesterday — it’s been a long day) with an interesting (and welcome) variation from the usual physics conference fare. Our opening keynote speaker was Bart Gordon, a former congressman from Tennessee who recently spent four years as the chairman of the House Committee on Science and Technology.

His actual speech seemed like standard “politician’s patter,” the sort of this that’s supposed to make you feel good but doesn’t say much concrete. At least, I’m not sure exactly what his point was. The interesting part was the Q&A session afterwards. Audience members asked some insightful questions about education, immigration, and so on, but mostly about keeping government funding for basic research, and generally ensuring that the sort of science we’re doing continues to have a place in society. What does it take to make this a talking point in the government?

Congressman Gordon responded with what I consider to be an important point: people have to talk to their local representatives. Lobbying 101, he said, is that you lean on the elected officials who actually represent you, because it’s their job …

I’m all settled in at the Omni Shoreham for Quark Matter 2012. First impression: this is by far the fanciest hotel I’ve ever stayed in. At least from the front, it’s basically everything you’d expect from a hotel that hosts presidential inauguration balls on a regular basis. The place looks like a giant medieval palace from the outside, but the front lobby is clearly designed to sell the image of luxury. I’m sure there are a number of extravagant suites somewhere in this place, but my guest room is pretty ordinary; still, tucked away in the back wing of the hotel, it runs $500 a night. It’s a pretty drastic (and, I’d say, welcome) change from the restricted budgeting we usually have to deal with in science.

As if that weren’t enough, they’re also giving us some cool swag. Everybody gets a themed backpack with a dedicated laptop pocket and cushioned case, a multipocketed ID holder on a lanyard, and a pen.

Anyway, the conference is kicking off with Student Day, which I expect to like because it’s probably going to be more comprehensible than most of the other stuff …

Updates on this blog have been kind of sporadic over the past couple months, I know. Part of the reason for that is that the posts I want to do involve some research which I haven’t entirely had time for, but besides that, I’ve also been busy preparing for my presentation at Quark Matter 2012! This is a physics conference that focuses on the study of the strong force in systems that contain lots of quarks and gluons — not just individual protons and neutrons, but entire atomic nuclei as well.

The particular piece of research I’ll be presenting is about the particle reaction \(\mathrm{p}A\to e^- e^+ \pi^0 X\): a proton collides with an atomic nucleus (the \(A\)) and produces an electron-positron pair, a pion, and other junk which we don’t care about (the \(X\)). The electron and positron themselves are produced from a (virtual) photon, so when you get down to the core of it, the reaction is really \(qg\to q\gamma^*\): a quark from the proton and a gluon from the nucleus interact to give a quark and a photon.

What we’re interested in is the angle between that …

Every once in a while I run across somebody on the internet trying to explain the meaning of “law” and “theory” in science. Usually they say something about how a law states a relationship between quantities whereas a theory tries to explain it, or vice versa, or that a law is older than a theory, or how a law is supported by different kinds of observations, or some such thing. While I appreciate that people are making the effort to discredit the idea that evolution isn’t accepted because it’s “just a theory,” I really think they’re going about it the wrong way.

The real difference between a law and a theory is much simpler: there is none. They’re just labels. They don’t mean anything.

Yes. there are some ideas in science that are traditionally called laws, and some that are traditionally called theories. It’s mostly a historical accident which are which. There are also ideas that go by either label with roughly equal frequency, or “law” sometimes and “theory” other times depending on context, or on who you’re talking to, or on something else. The point is, there’s no consensus in the …