Why, oh Y(4140) are you so tantalizing?
Posted by David Zaslavsky on — EditedNote: I’m posting this from the road, so it will be somewhat lacking in pictures and details. Stay tuned for an update that fills all that in!
I’ve spent a lot of time poring over the results coming out of the Hadron Collider Physics conference this week, and I’ve noticed a trend. Higgs candidate cross sections are consistent with the standard model. B meson branching ratios are consistent with the standard model. Multijet event counts are consistent with the standard model. Maybe you can see where this is going. Vector boson production rates are consistent with the standard model. CMS rediscovered an unknown particle. Meson masses are consistent with—
Wait, what?
Yeah, that happened. CMS announced the second observation ever [PDF] of a mysterious new particle which defies classification.
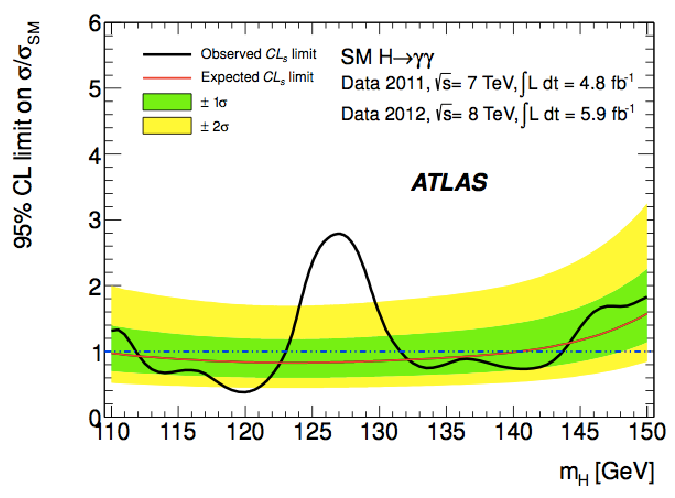
This mystery object, called the Y(4140) or sometimes X(4140), was first seen in 2009 by CDF, one of the experiments at the Tevatron. It wasn’t just a slight fluctuation, either; the CDF data excluded the background-only hypothesis at more than a 5σ level, which is the threshold physics uses to define a proper discovery. Certainly much ado has been made about less strong statistical …