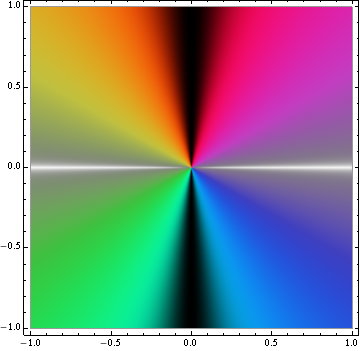
In the process of graphing some complex valued functions, I figured out a couple of neat coloring schemes that I thought might be worth sharing. Both schemes share the same hue and saturation functions:

They differ in the third component, though. The one which I will arbitrarily designate “color scheme 1” (because I like it better) is defined in HSL color space, and has a luminosity function of

where \(S\) is the saturation value. This maps all real or nearly real numbers to white, all imaginary or nearly imaginary numbers to black, and other complex numbers to varying hues depending on their phase.

The other one, “color scheme 2,” has a value (brightness) function of

This maps all real or nearly real numbers to white, and all other numbers to varying hues, again depending on their phase. Positive imaginary numbers are red, negative imaginary numbers are cyan.

Note that both functions are undefined at \(z = 0\). If you implement these you …